1  引言
    伴随着列车“高速度、高密度运行”新形势的飞速发展，以及全国铁路6次大提速中出现的“单司机、长交路”等新情况，如何在保证安全的前提下提高铁路运营管理水平已成为铁路发展的当务之急。为了保证列车的行车安全、提高列车运行效率，研究列车速度控制并得到满意的控制效果是非常必要的。而列车的运行过程是极其复杂的，不确定因素多且离散性大。对列车运行过程进行安全有效的控制仍是铁路自动化领域一直未能很好解决的焦点问题之一。因此关于列车速度控制方法的研究对铁路运输具有十分重要的意义。然而原有的列车速度控制方法难以满足安全行车要求。因此本文采用的预测控制可以根据以后的输入对控制参数和控制策略进行有计划的调整，降低了控制量的时滞，提高了列车的控制效果和控制效率。预测控制利用在线估计预测模型，减少了由于模型不准确带来的误差，使得模型具有实时性。由于预测控制采用在线滚动优化指标和反馈校正策略，使系统具有较好的稳定性和鲁棒性。

2  列车速度控制数学计算模型
2.1 列车的运动方程
    列车是在具有坡道和弯道的轨道上依靠机车的粘着牵引力行驶的，由于驾驶坡道的长度远远大于列车的车长，可将列车作为一个质点处理，其运动方程可用牛顿第二定律表示如下：
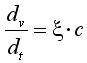                       (1)
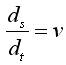                       (2) 
    式中：c—作用于列车上的单位合力(kn)；
          v—列车运行速度(m/s)；
          s—列车走行距离(m)；
    因为单位合力不是常数，上述方程无法直接求解。试着用逼近法求解：假设列车在一段很小的计算时间间隔△t内单位合力为常数，可得：
    c =f(v₁,s₁,u₁)－w(v₁,s₁)             (3)
    式中：f(v₁,s₁,u₁)，w(v₁,s₁)分别为在速度v₁、位置s₁、手柄级位u₁时的总牵引力(包含制动力，制动力为负)和总阻力。
    因为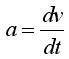加入式可得：
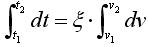                               (4)
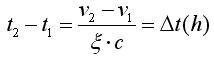                   (5)
    已知v₁，根据式(2)近似地求出这一段的c，根据式(4)可求出v₂，如此向前推算，可以画出列车运行的速度——距离曲线。其中△t取得越小，计算精度越高。
2.2 列车制动距离计算
    (1)空走距离
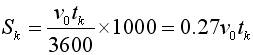               (6) 
    式中：v₀—制动初速；
          t_k—空走时间。
    (2)有效制动距离
    用分析法可得分速度间隔的间隔距离为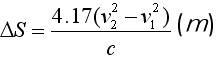：(m)    (7) 
    有效制动距离为：
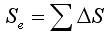       (8) 
    用上式计算有效制动距离时，通常每个速度间隔不超过10km/h。

3  列车速度控制预测模型
    假设在时刻k有u(k)为控制输入，s(k)为当前位置，v(k)为当前速度。根据式(2)求得列车的合力c，根据式(4)可以确定：
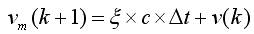               (9) 
    列车运行单步输出预测模型为：
    v_m(k+1)=g(v(k), u(k), s(k))        (10) 
    式中：g(v(k), u(k), s(k))为函数表达式，表明vm(k+1)是v(k), u(k), s(k)的合成函数。由式(9)递推叠代的方法可以得到列车多步的运行速度输出预测公式：    
    v_m(k+p△t) = g(v(k+(p－1)△t),…,v(k+(p－(p－1)△t)),v(k), u(k), s(k) (11)
    式中：p—预测步数；
        △t—采样时间。
    根据预测模型引入实际模型与预测模型当前输出之间的偏差进行修正，修正后的1步预测输出为：
    v_p(k+1)= v_m(k+1)+h(v(k)－v_m(k))
           = v_m(k+1)+ he(k)           (12)
    其中：e(k)—实际模型和预测模型k时刻的误差；
             h—误差修正系数。
    我们可确定预测误差的目标函数为：
    j_p=[v_p(k+1)－v (k+1)]²           (13) 
    取滚动优化中的优化性能指标为：
    j_p=[v_p(k+1)－v (k+1)]²             (14)
    根据优化性能指标求取最优控制量：
    令 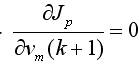        (15)
    得v_m(k+1)+he(k)－v(k+1)=0     (16)
    即v_m(k+1)= v(k+1)－he(k)        (17)
    这里 v_m(k+1)=△u(k)                (18)
    所以，最优控制变化量为：
      △u(k)=v(k)+he(k)                  (19)

4  列车速度预测控制算法
    列车速度预测控制过程示意图如图1所示。系统的控制过程以一个闭塞区间为单位进行。图中v_in为列车的入口速度；v_out为列车运行出口速度；s(k)为制动区，它是由预测模型根据线路条件、入口/出口速度，以标称减压量计算出来的；s(k+α△t)为一个控制时间α△t(α为控制时间常数)内的列车运行距离；s_max为实施上一个控制时间后，由预测模型计算出来的余下运行时间内的列车制动距离。△s为安全防护距离(货车为100m，客车40m)。这里的标称减压量随着速度的高低有所不同。

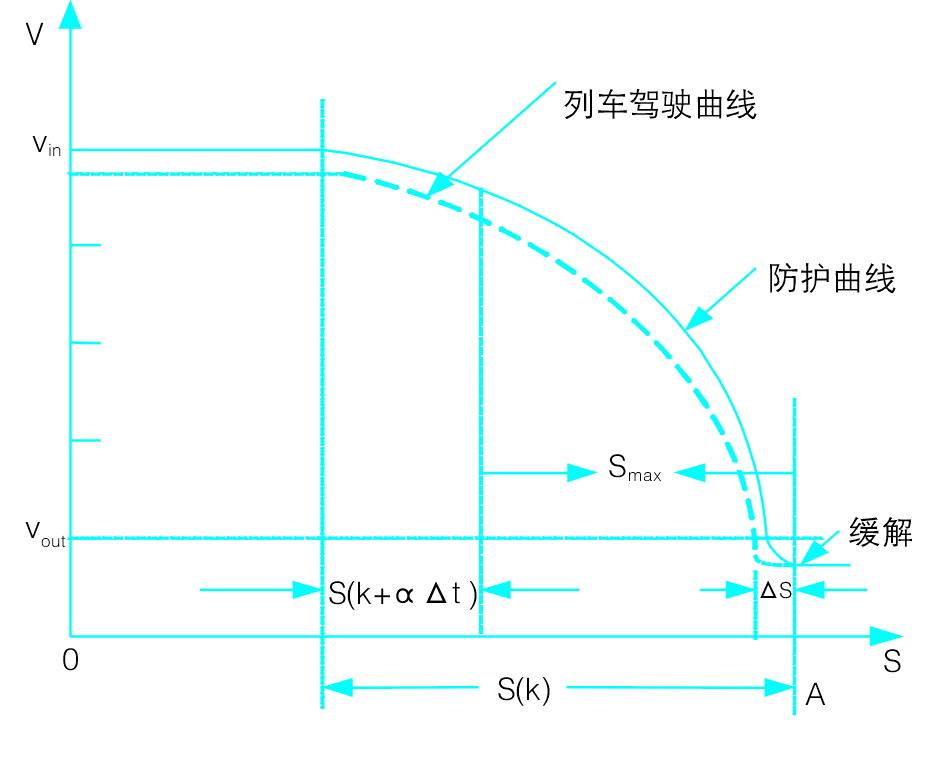
图1  速度预测控制过程示意图

5  仿真实验与结果分析
    以兰州-定西铁路线路为实验线路，选取骆驼巷-桑园子一个闭塞区间研究列车的速度预测控制并进行系统仿真。线路具体参数如下：线路全长1.9km，最高限速为100km/h，允许速度为60km/h，限制慢行速度为30km/h，平均坡度为6‰，曲线半径为r680。机车型号为ss3b型，载重4000t，编组50辆，列车管压500kpa，采用高磷闸瓦。
    根据列车运行特点，利用预测控制方法对列车运行速度设计仿真程序，利用matlab软件仿真。仿真结果如图2、图3、图4所示。

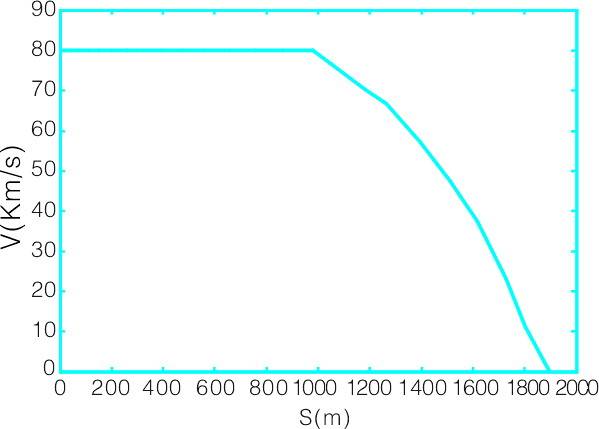
图2  列车常规制动速度-距离控制曲线

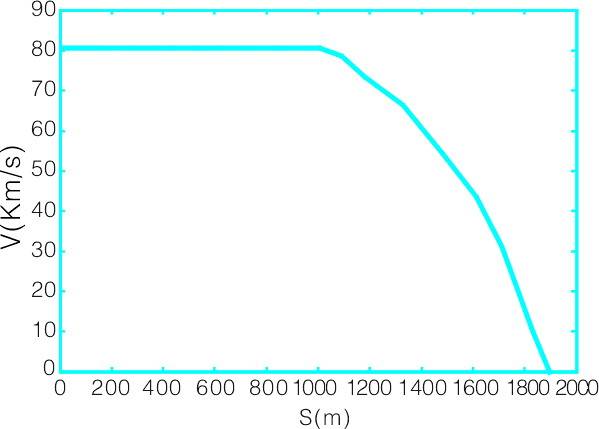
图3  基于预测控制的列车速度-距离曲线

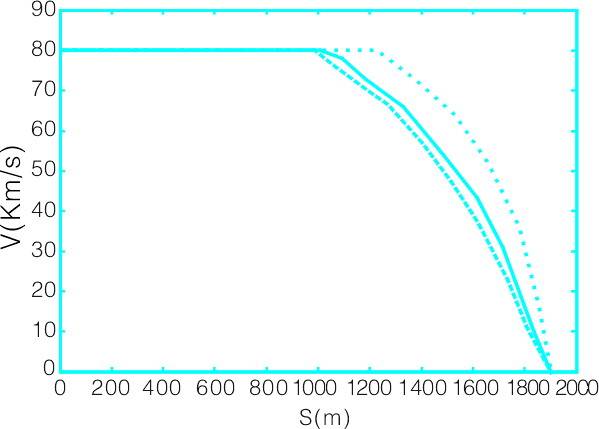
图4  同车同速、不同控制方法制动曲线图

    列车速度控制曲线如图2所示。列车在979.2m开始实施制动，在此之前进行速度为80km/h的匀速运动。然后列车开始进行加速度不等的减速运动。列车在1.9km处速度为0。
    列车速度预测控制曲线如图3所示。列车在距列车在1030m开始实施制动，在此之前进行速度为80km/h的匀速运动。因为列车的阻力与列车速度有关，所以在不同速度时刻列车的阻力不同，列车的加速度也不同，列车运行是一变桨加速度运动。列车在1.9km处速度为0。图中横坐标为列车运行预测控制的距离，纵坐标为列车运行速度。
    图4为同车同速、不同控制方法制动曲线图。图中横坐标为列车运行控制的距离，纵坐标为列车运行速度。预测控制列车速度在制动过程中小于防护速度，大于列车常规制动速度。说明列车速度预测控制方法优于常规制动。

作者简介
    邱亚娟(1983-)  女  硕士研究生，研究方向为伺服电机控制技术。

参考文献 (略)